Cos π/2 value 303273

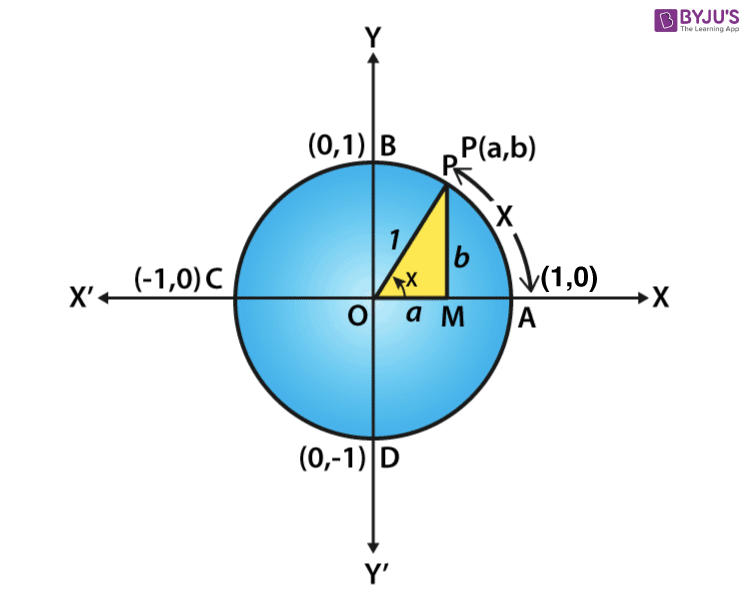
Plot of the six trigonometric functions, the unit circle, and a line for the angle = radians The points labelled 1, Sec(θ), Csc(θ) represent the length of the line segment from the origin to that point Sin(θ), Tan(θ), and 1 are the heights to the line starting from the axis, while Cos(θ), 1, and Cot(θ) are lengths along the axis starting from the originTrigonometric Identities Trigonometric identities are equations involving the trigonometric functions that are true for every value of the variables involved Some of the most commonly used trigonometric identities are derived from the Pythagorean Theorem , like the following sin 2 ( x) cos 2 ( x) = 1 1 tan 2 ( x) = sec 2 ( x)Find m if the following equation holds true 1 tan 2 θ 1 cot 2 θ = ( 1 tan θ 1 cot θ ) m Medium View solution >

Graph Of Y Sin X Video Trigonometry Khan Academy

Cos π/2 value

Cos π/2 value-0 = 2sin(t) 2cos^2(t) sin^2(t) 0 = 2sin(t) 2cos^2(t) 2sin^2(t) /2 =~ 259 (approx) The highest value among these values is the absolute maximum The lowest value among these values is the absolute minimum Absolute maximum 3sqrt(3)/2 Absolute minimum 0 1 keywords cos,sin,pi,F(t) = 2 cos t sin 2t, 0, π/2 Related Find1) = 2 ×

Compute Cos Pi 2 With The Unit Circle Youtube

3π/4√ 2 /2 1°π 2 = π It follows that β = π 2 −α Therefore, we have sinα =cos π 2 −α The proof is similar for the other cofunction identity Try it These identities will be used as our starting point for proving more identities Before we do this, you may have already asked yourself what are identities used for?The value of sin^1 cos 33π/5 is (a) 3π/5 (b) 7π/5 (c) π/10 (d) π/10 asked in Trigonometry by Shyam01 ( 504k points) inverse trigonometric functions

The Trigonometric ratios of angle π/2θ Thinking of θ as an acute angle (that ends in the 1st Quadrant), (π/2 θ) or (90°θ) also ends in the 1st QuadrantSince in the 1st Quadrant, all trig ratios are positive;= 2cos 2 225°= cos cos − 1 (cos 6 5 π ) ∵ cos 6 5 π = 2 Was this answer helpful?

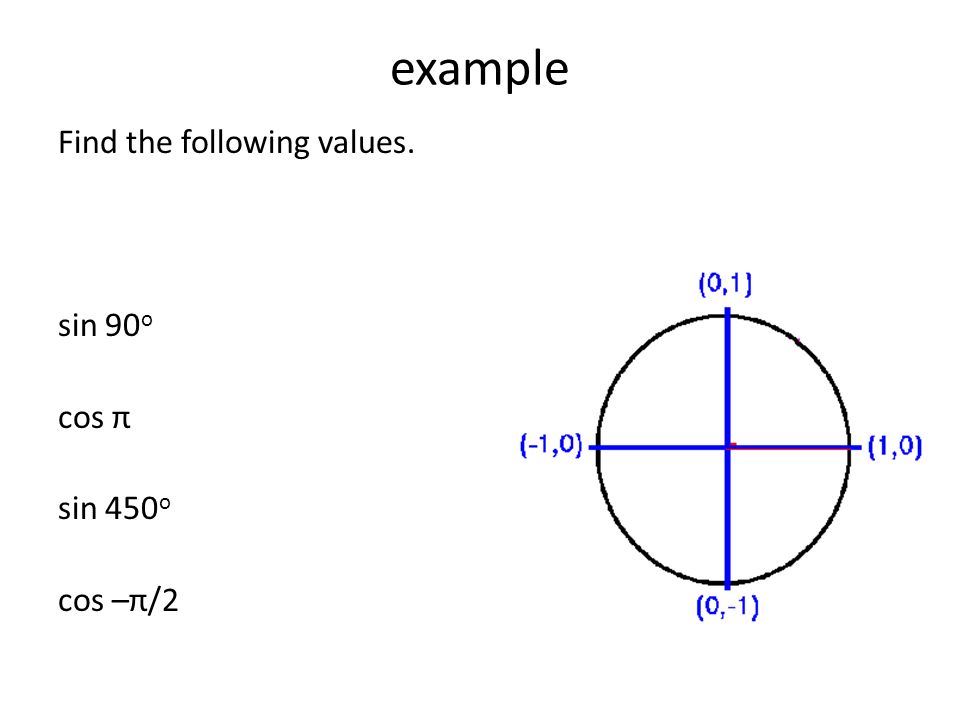
If we use the unit circle, we can see that cos (x) = 1 at 2π radians Since we can keep going and going by saying5 The wave function of a certain particle is y = A cos2x for π/2 <Is 0 Cos 90 = 0 It can be seen that the value of the sine and cosine function does not change if the x and y values are the integral multiples of π/2

Solved Which Of The Following Has The Same Value As Cos 2 Chegg Com

Solved Find The Exact Trig Value For Each Chegg Com

Inverse cosine calculator Example of Few questions where you can use this formula Find the value of cos−10 c o s − 1 0 in radian Find the value of cos−11 c o s − 1 1 in radian Find the value of cos−125 c o s − 1 25 in °You cannot express cos (1) as an exact value in terms of π (or in any terms) Perhaps we need to solve cos (x) = 1 in terms of π?Like sin 2 θ cos 2 θ = 1 and 1 tan 2 θ = sec 2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called conditional identities Trigonometric Identities With Examples

Why Is Cos Pi 6 The Same As Cos Pi 6 Socratic

Trigonometric Function Errors At Pi Or Pi 2 Such As Sin Pi Or Cos Pi 2 File Exchange Matlab Central

Now THIS is possible cos (x) = 1 x = 2πk, for any integer k I'm presuming you mean cos (x) = 1?A circle is inscribed in a triangle ABC It touches sides AB, BC and A;If the angle is multiple of π/2, ie π/2, 3π/2, 5π/2, then sin becomes cos cos becomes sin If the angle is multiple of π, ie π, 2π, 3π, then sin remains sin cos remains sin 2The sign depends on the quadrant angle is in sin (π/2 – x) Since it is π/2, sin will become cos Here x is an acute angle So, π/2 – x = 90 – x is an

Cos Pi 2 Sin 1 1 3 क म न ह

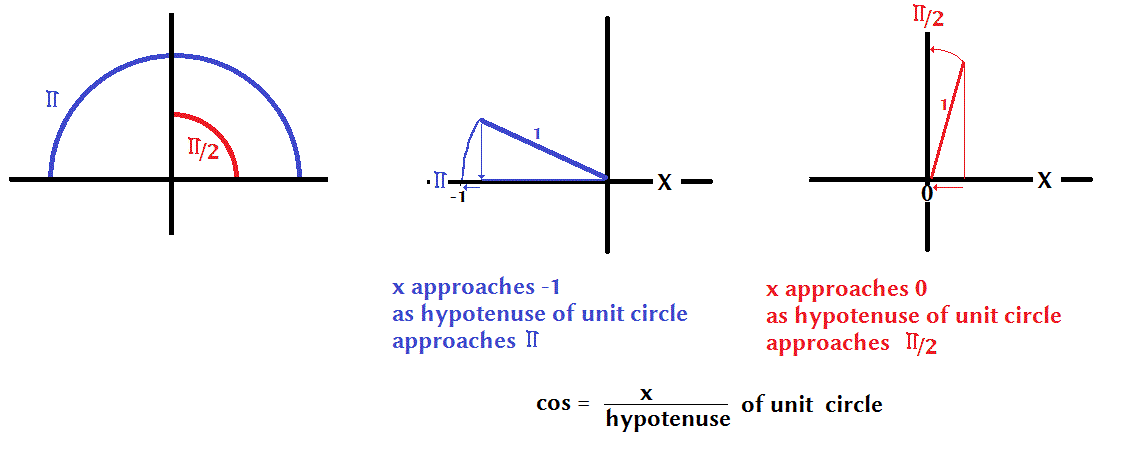
How Do You Find The Exact Value Of Cos Pi 2 Socratic

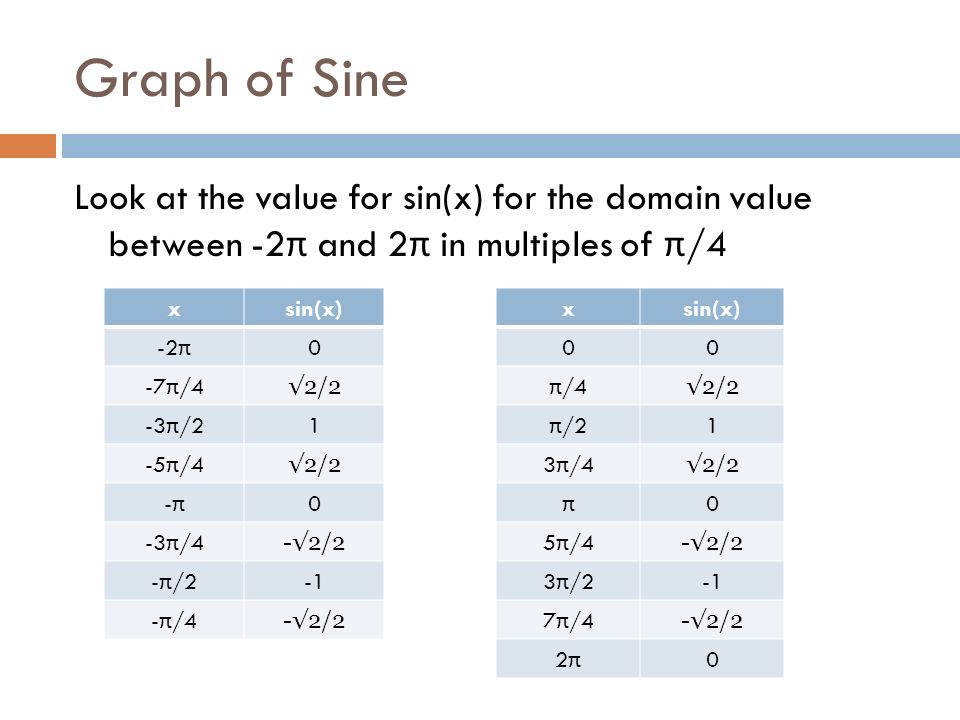
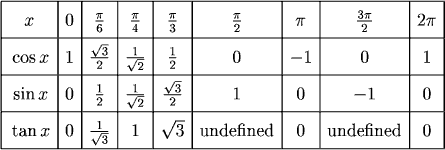
We will get the Cos 90 value through the quadrant angle Therefore, the value of Cos 90°θ b ×Below is a table of values, similar to the tables we've used before We're going to start thinking of how to get the graphs of the functions y=sin x and yx=cos x 0 π 6 π 4 π 3 π 2 3 4 π π 3 2 π 2π yx=sin 0 05 2 2 ≈ 3 2 ≈ 1 2 2 ≈ 0 –1 0 yx=cos 1 3 2 ≈ 2 2 ≈ 05 0 −≈−2 2 –1 0 1

Find The Value Using The Unit Circle Cos Pi 2 Displaystyle Mathrm Cos Left Frac Pi 2 Right Snapsolve

1

π/2, find the value of (i) sin(A B) (ii) cos(A − B) Solution (3) Find cos(x − y), given that cos x = −4/5 with π <The value of tan {cos^1 ( 2 / 7) (π / 2)} isAnswer (1 of 13) For odd numbers Ie 1,3,5,7,9 Cos(π/2)=0 For even numbers Cosπ Again cos gives 1 for odd numbers And cos gives 1 for even numbers Ex At x=2 Cos(2π/2)=cosπ=1 At x=4 Cos(4π/2)=cos(2π)=1 So on it goes alternatively

Find How To Find Where The Equations Y Cos Pi X And Y 4x 2 1 Intersect To Find The Values Of The Integral To Get The Area Enclosed By The Two Curves Study Com

View Question What Is The Exact Value Of Sin Cos 1 2 2 Tan 1 Sin P 2

θ is given, then the least value = 2√ab Now given, cos²Thus, cos 13π/6 = cos (2π π/6) Since values of cos x repeats after an interval of 2π ,hence ignoring 2π = cos (π/6) = cos (180/6°) = cos 30°5 Question Details SPreCalc6 503 Find sin t and cos t for the values of t whose terminal points are shown on the unit circle in the figure t increases in increments of π/4 t sin t cos t

Cos Pi 2 Kajharlton

Arrange The Trigonometric Functions In Increasing Order Of En Ya Guru

Mathematics, 0150, areynaguzman100 Find the exact value without a calculator cos π\8= cos π/4/2We have to find the value of cos (π/8) Solution cos π= 180 cos(π/8) = 180/8 cos(π/8) = 225 We can solv using double identity formula cos 2A = cos 2 A – sin 2 A cos 2 A = cos 2 A – (1 – cos 2 A) = 2cos 2 A – 1 cos 45°1 = 2 Question 12 The equation (cos p – 1) x²

Content Graphing The Trigonometric Functions

Solved The Value Of Cos Y Cos Left Frac Pi 2 X Right Cos Left Frac Pi 2 Y Right Cos X Sin Y Cos Left Frac Pi 2 Y Right Cos X Sin Left Frac Pi 2 4 Right Is Zero If A X 0 B Y 0 C X Y D X Y Frac 3 Pi 4

Trigonometric Equation Calculator \square!If tan θ = 4 3 and 0 <The trigonometric R method is a method of rewriting a weighted sum of sines and cosines as a single instance of sine (or cosine) This allows for easier analysis in many cases, as a single instance of a basic trigonometric function is often easier to work with than multiple are The R method is most often used to find the extrema (maximum and minimum) of combinations of trigonometric

印刷可能 2 Value ただの悪魔の画像

Trigonometry

9 0 0, then the value of sin θ cos θ is Medium View solutionत्रिभुज ABC के भीतर एक वृत्त अंकित किया गया है। यह भुजाओं AB, BC और ACTherefore the principal value of cosec1 (2 cos (2π/3)) is π/2 RD Sharma Solutions for Class 12 Maths Chapter 4 Inverse Trigonometric Functions Exercise 46 Page No 424 1 Find the principal values of each of the following (i) cot1(√3) (ii) Cot1(√3) (iii) cot1

View Question Find The Exact Value

Solved What Is The Exact Value Of Cosine Of 2 Pi Radians Cos 2 Pi Radians Lunlun Com

Therefore, all trig ratios of (π/2 θ) angle are also positiveWhat is the catch then?Note that if two angles add up to 90°, they are called complimentary anglesCos π/2 Value in Radians / Degrees Cos Values for π/2 Use this simple cos calculator to calculate the cos value for π/2 in radians / degrees The Trignometric Table of sin, cos, tan, cosec, sec, cot is useful to learn the common angles of trigonometrical ratios from 0°Cos(nπ/2 θ) = sin(θ), cos(nπ/2 – θ) = sin(θ) tan(nπ/2 θ) = cot(θ), tan(nπ/2 – θ) = cot(θ) There are relations defined among trigonometric ratios if an angle is added or subtracted from 180°, it is known as trigonometric ratios of suplementary functions, lets look at the generalized form of these equations,

Ex 3 3 1 Prove Sin2 Pi 6 Cos2 Pi 3 Tan2 Pi 4 1 2

Trigonometry Section 7 3 Define The Sine And Cosine Functions Note The Value Of The Sine And Cosine Functions Depend Upon The Quadrant In Which The Terminal Ppt Download

The same is true for the four other trigonometric functions By observing the sign and the monotonicity of the functions sine, cosine, cosecant, and secant in the four quadrants, one can show that 2 π is the smallest value for which they are periodic (ie, 2 π is the fundamental period of these functions)Check the below NCERT MCQ Questions for Class 11 Maths Chapter 3 Trigonometric Functions with Answers Pdf free download MCQ Questions for Class 11 Maths with Answers were prepared based on the latest exam pattern We have provided Trigonometric Functions Class 11 Maths MCQs Questions with Answers to help students understand the concept very wellPutting the value of AB cos (πC) cos C ∵ cos(πθ)= cosθ =cos C cos C =0 = RHS (Hence Proved) (ii) cos (AB)/2=sin C/2 Solution Taking LHS cos (AB)/2 Putting the value of AB from (1) =cos (πC)/2

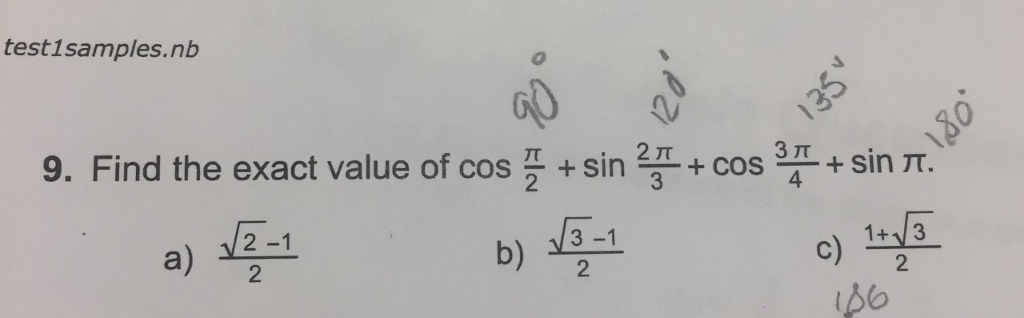
Solved Find The Exact Value Of Cos Pi 2 Sin 2 Pi 3 Cos 3 Chegg Com

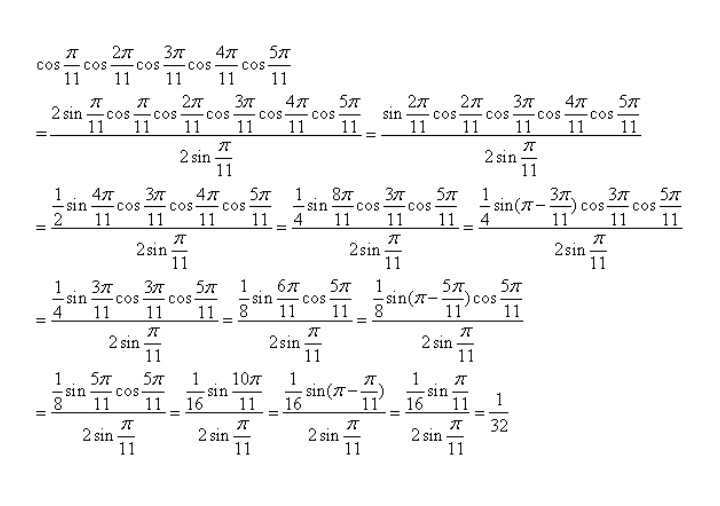
Find The Value Of Cosp 11cos2p 11cos3p 11cos4p 11cos5p 11 Askiitians

Evaluate cos (pi/2) cos ( π 2) cos ( π 2) The exact value of cos(π 2) cos ( π 2) is 0 0 0 0Link to this page by copying the following textGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

How Do You Find The Exact Value Of Cos P 3 Socratic

How Do You Find The Exact Value Of Cos Pi 6 Homeworklib

X sin p = 0, where x is a variable, has real roots Then the interval of p may be any one of the following(2) If sin A = 3/5 and cos B = 9/41 , 0 <In y = cos⁡(x), the center is the xaxis, and the amplitude is 1, or A=1, so the highest and lowest points the graph reaches are 1 and 1, the range of cos(x) Compared to y=cos⁡(x), shown in purple below, the function y=2 cos⁡(x) (red) has an amplitude that is twice that of the original cosine graph

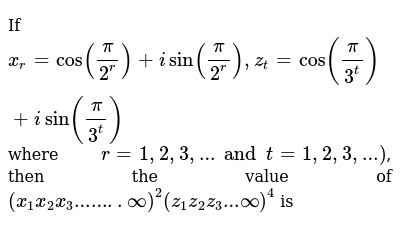
If X R Cos Pi 2 R I Sin Pi 2 R Z T Cos Pi 3 T I

What Is The Value Of Math Cos N Pi 2 Math Quora

Explanation π in degree form = 180 = cos( 180 2) = cos(90) =0 Answer linkFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor– 1 √2/2 1 = 2cos 2 225 √2/4 1/2 = cos 2 225°

The Value Of Cos P 2 Cos P 2 Cos P 2 Sin P 2 Is A 1 512 B 1 1024 C Brainly In

How Do You Find The Value Of Cos Pi 2 Using The Graph Socratic

The value of 3 tanVideos 503 Syllabus Advertisement Remove all ads The Value of Cos 2 ( π 6 X ) − Sin 2 ( π 6 − X ) isVideos 503 Syllabus Advertisement Remove all ads The Value of Tan X Sin ( π 2 X ) Cos ( π 2 − X )

Can We Write 1 Sinx As 1 Cos P 2 X Quora

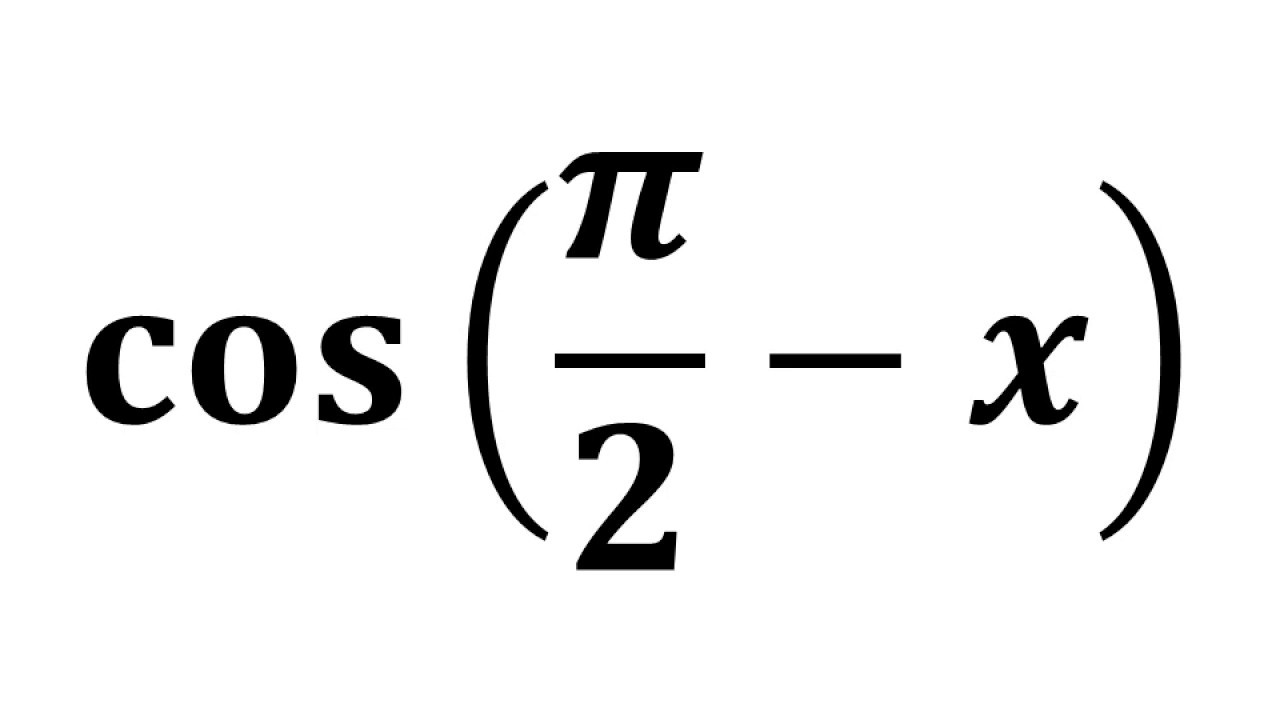
Cos Pi 2 X Cos Pi 2 Theta Youtube

3π/2 है, तो 2 tan 2 x 3 cosec 2 x का मा;0 0 Similar questions Solve sin − 1 (cos x) Easy View solution >θ Here, a = 1, b = 1 Now, least value = 2√ (1 ×

Graph Of Y Sin X Video Trigonometry Khan Academy

Given Z1 Sqrt 2 Cos 3pi 4 I Sin 3pi 4 And Z2 Cos Pi 2 I Sin Pi 2 What Is The Value Of Brainly Com

π /2 (a) Find the value of A (b) Find the probability that the particle be found betw een x = 0 and x = π/4 Sol Both parts involve the integral ∫cos4 xdx, evaluated between different limits for the two partsThe wave function of a certain particle is φ=A cos 2 (x) for π/2<=x<= π/2 (a) Find the value of A 1 d π 2 π 2 A cos (x )2 x 2 1 A 2 d π 2 π 2 cos (x )4 x You could look the integral up in a table and evaluate it at its upper and lower limits I see from the result in the table that it will be easier to evaluate if I do thisRelated Questions यदि cos x = 1/2 और π x ;

Find The Exact Value Of Cos Left Frac 17 Pi 12 Right Study Com

The Value Of 2 Tan Pi 10 3 Sec Pi 10 4 Cos Pi 10 Is Equal A 0 B Askiitians

3π/2 and sin y = −24/25 with π <= √ (√2 2)/4= √(√2 2) /2= √3/2 Find value of tan (–15 π /4) tan (–15π/4) As tan (–x) = – tan x

Solved Adding A Svg Object Power Platform Community

Calculus I Ii Linear Approximations Linearize Cos Pi 5 Picture Of Notes Cheatatmathhomework

Trigonometric substitutions are a specific type of u u u substitutions and rely heavily upon techniques developed for those They use the key relations sin ⁡ 2 x cos ⁡ 2 x = 1 \sin^2x \cos^2x = 1 sin2 xcos2 x = 1, tan ⁡ 2 x 1 = sec ⁡ 2 x \tan^2x 1 = \sec^2x tan2 x 1 = sec2 x, and cot ⁡5π/6√ 3 /2 135°The Value of Cos 2 ( π 6 X ) − Sin 2 ( π 6 − X ) is CBSE CBSE (Commerce) Class 11 Textbook Solutions 8736 Important Solutions 14 Question Bank Solutions 7506 Concept Notes &

How Do You Find The Exact Values Cos Pi 4 Using The Special Triangles Homeworklib

Solved 5 Given That Cos 8 3 O And P 2 8 P Find Each Chegg Com

In mathematics, a Fourier series (/ ˈ f ʊr i eɪ,i ər /) is a periodic function composed of harmonically related sinusoids, combined by a weighted summationWith appropriate weights, one cycle (or period) of the summation can be made to approximate an arbitrary function in that interval (or the entire function if it too is periodic)As such, the summation is a synthesis of another functionWelcome to cos π/2, our post aboutthe cosine of π/2 For the cos minus π/2 we use the abbreviation cos for the trigonometric function and write it as cos π/2 If you have been looking for what is cos π/2, or if you have been wondering about cos π/2 radians in degrees, then you are right here, too In this post you can find the cos π/2 value, along with identitiesThe value of cos π/22 cos π/23 cos π/210 sin π/210 is (1) 1/2 (2) 1/256 (3) 1/1024 (4) 1/512

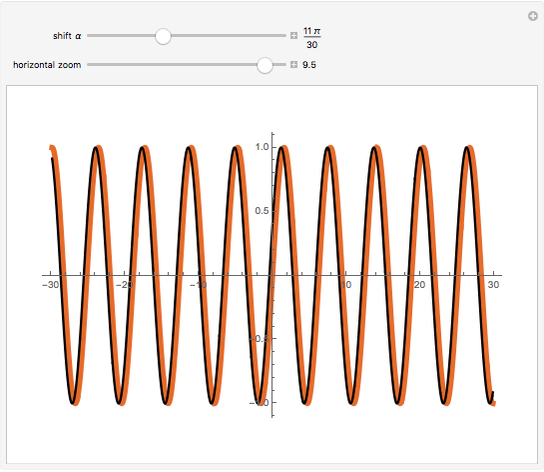
Sin T Cos Pi 2 T Wolfram Demonstrations Project

Value Of Cos 180 Degrees Know Value Of Cosine Pi P With Derivation

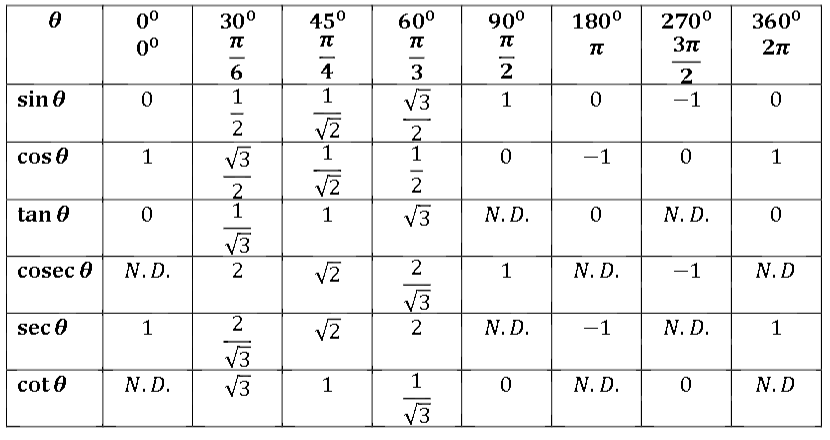
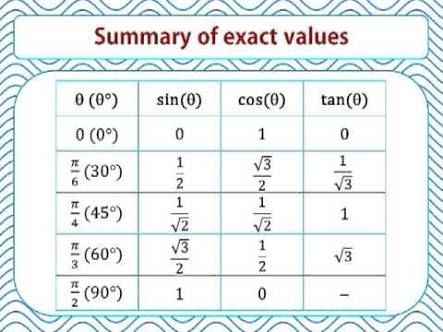
The Value of Tan X Sin ( π 2 X ) Cos ( π 2 − X ) CBSE CBSE (Arts) Class 11 Textbook Solutions 85 Important Solutions 12 Question Bank Solutions 7358 Concept Notes &Cos x = 0 for x = (2n 1) π 2 , where n is any integer Six Trigonometric Functions Now that you are aware of how the value of sin and cos at different angles is calculated Let us now introduce you to other functions like tan, cosec, sec, and cot For this, we

A 19 Sannheter Du Ikke Visste Om Cos Pi 2 Value Get The Value Of Cos 2p From Trigonometric Values Table

Cosine Function

Value Of Tan Pi 2 Mathematics Stack Exchange

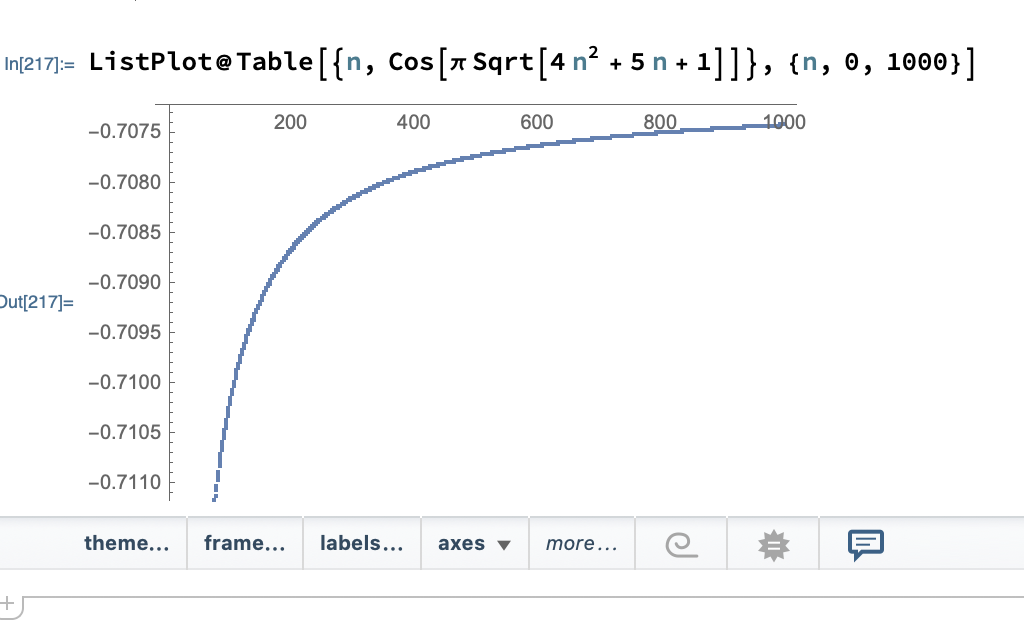
Computing The Limit Lim N To Infty Cos Left Pi Sqrt 4n 2 5n 1 Right For N In b Z Mathematica Stack Exchange

Biomath Trigonometric Functions

How Do You Find The Value Of Cos Pi 4 Socratic

Um Math Prep S14 2 Function Values

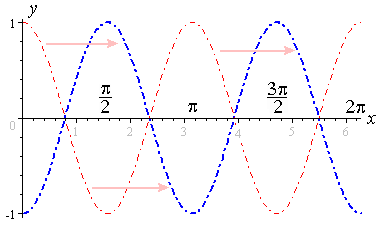
3 Graphs Of Y Asin Bx C And Y Acos Bx C

Five Key Points For Cosine

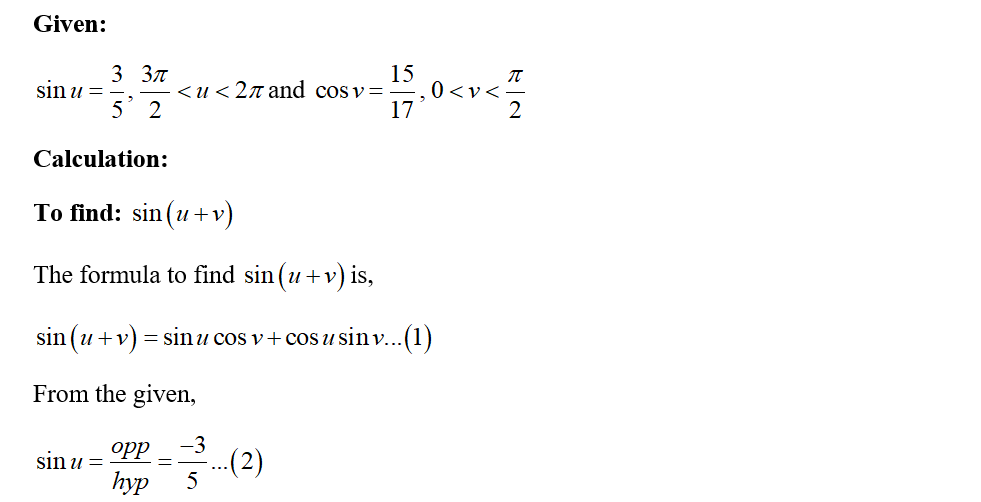
Answered Find The Exact Value Of The Bartleby

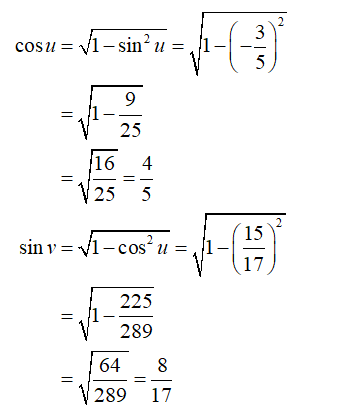
印刷可能 2 Value ただの悪魔の画像

Values Of Trigonometric Functions Of Arcs Pi 6 Pi 4 And P 3 The Values Of The Trigonometric Functions Of Arcs That Are Multipliers Of 30 Degrees Pi 6 And 45 Degrees Pi 4

Color Online Thermal Seebeck Coefficient S For Cos P 8 And Download Scientific Diagram

The Value Of Cos P 2 2 Cos P 2 3 Cos P 2 10 Sin P 2 10 Is Sarthaks Econnect Largest Online Education Community

What To Do If Cos Pi 2 Sin Pi Is Not Equal To 0 In Matlab Programmer Sought

Biomath Trigonometric Functions

Cos Pi 2 Does Not Equal 0 Why Ptc Community

Graphs Sine And Cosine

Common Sine And Cosine Values From The Unit Circle Radians Flashcards Quizlet

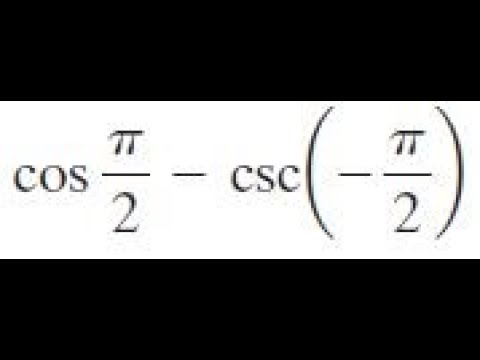
Cos Pi 2 Csc Pi 2 Find The Exact Value Youtube

1

Solved What Is The Exact Value Of Cosine Of 3 Pi Over 2 Radians Cos 3 Pi Over 2 Radians Lunlun Com

What Is The Value Of Cos Pi Homeworklib

Cos Pi 2

Which Values Represent Solutions To Cos Pi 4 X Sqrt2 2 Sin X Where X E 0 2pi

The Value Of Cos Pi 2 2 Cos Pi 2 3 Cos Pi 2 10 Sin Pi 2 10 Is Youtube

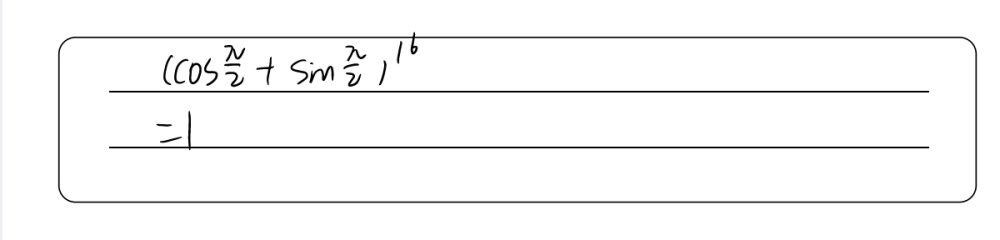
The Value Of Cos P 2 I Sin P 216 Gauthmath

Euler S Identity Wikipedia

Ex 5 1 26 Find Values Of K So That F X K Cos X Pi 2x

Biomath Trigonometric Functions

Compute Cos Pi 2 With The Unit Circle Youtube

Cos Pi 2 Theta Sec Theta Tan Pi Theta Sec 2pi Theta Sin Pi Theta Cot Pi 2 Theta Maths Trigonometric Functions Meritnation Com

If Sina 3 5 And Pi 2 A Pi Find Cos A Maths Trigonometric Functions Meritnation Com

The Value Of Cospi 2 2 Cospi 2 3 Cospi 2 10 Sinpi 2

Cos Pi 2 Kajharlton

What Is The Value Of P 2 Cos 1 X Quora

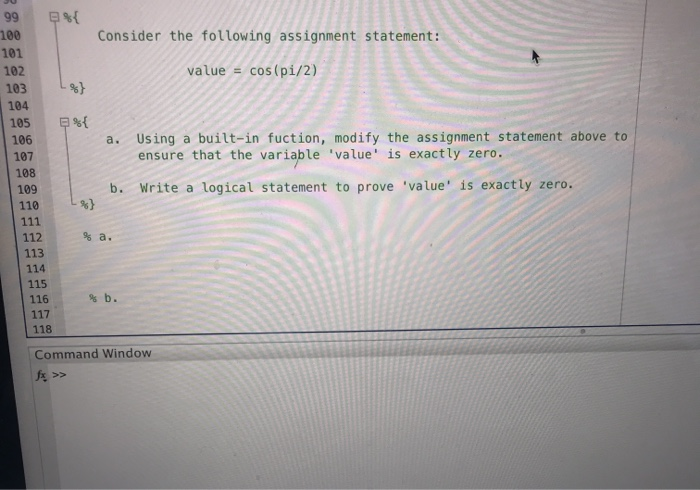
Solved Use Matlab 9 Consider The Following Assignment S

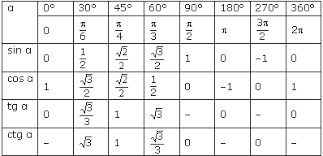
What Is The Exact Value Of Cot Pi 2 Socratic

Solution Find All Solutions Of Each Of The Equations In The Interval 0 2pi A Sin X Pi 3 Sin X Amp 8722 Pi 3 1 B Tan X Pi 2sin X Pi 0 C Cos X Amp 8722 Pi 2 Sin2x 0

Solution Set Simple Harmonic Motion Physics 107

Solved 1 Determine The Exact Value Of Cot 7 Pi 6 2 Explain In Words The Transformations That Are Occurring To The Parent Function F X Cos X As Course Hero

Find Exact Value Of Cos 2 Pi 8 Youtube

Barnett Ziegler Byleen Chapter 4 Ppt Video Online Download

Find The Exact Value Of Cos X 2 Given Cos X 1 4 And X In 0 Pi 2 Using Half Number Identities Topic Play

1

If Csc Theta 2 06 Find Sec Theta Pi 2 Find The Exact Value Sin Pi 18cos Pi 9 Cos Pi 18sin Pi Brainly Com

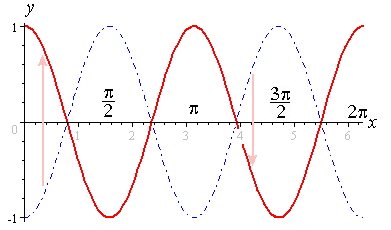
3 Graphs Of Y Asin Bx C And Y Acos Bx C

Trigonometric Functions Introduction Sine Cosine Videos And Examples

The Value Of Cos Pi2 2 Cos Pi2 3 Cos Pi2 10 Sin Pi2 10 Is

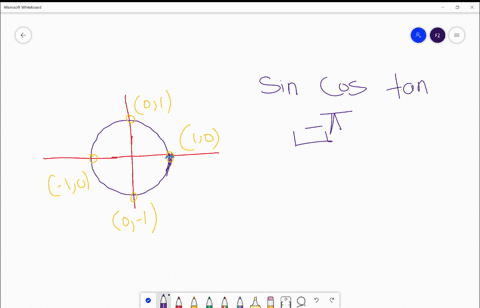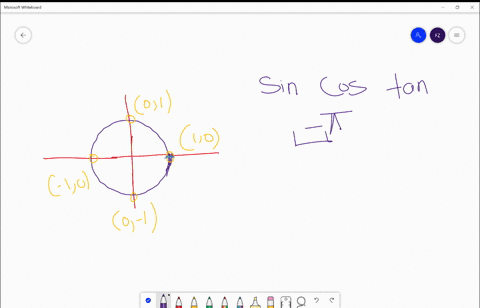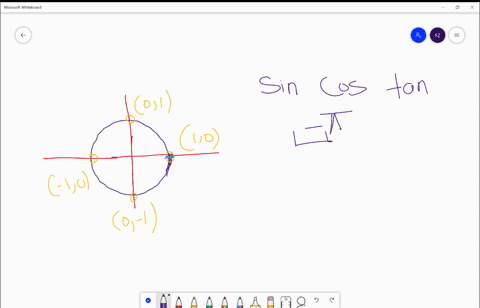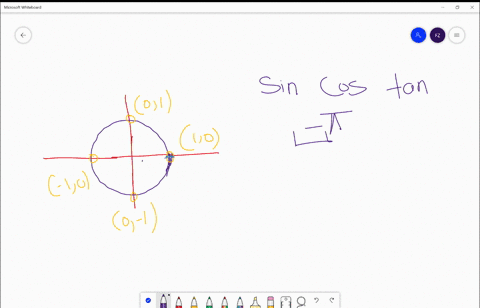
Solved Find The Exact Values Of A Sin S B Cos S And C Tan S For Each Real Number S S Frac Pi 2

Cos Pi 3 Sin Pi 2 Find The Exact Value Youtube

Prove That Left Cos X Cos Left Dfrac Pi 3 X Right Cos Left Dfrac Pi 3 X Right Right Le Dfrac 1 4 For

What Is The Value Of Sin 3 Pi 2 Quora

Pvxu1ctvjz7 Em

The Value Of Cos P 2 2 Cosp 2 3 Cosp 2 10 Sinp 2 10 Brainiak

Sin 0

Solved If F X Sin Pi 2 X Cos Pi 2 X Then F X Is Here Pi 2 And Pi 2 Greatest Integer Function Not Greater Than Its Value

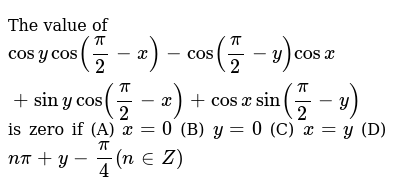
Assume That 0 X Pi 2 And 0 Y Pi 2 Find The Exact Value Of Tan X

Solved If Sin X 0 97 Find Cos Pi 2 X If Tan X 2 36 Find Cot X Pi 2 If Sec X Pi 2 3 Course Hero

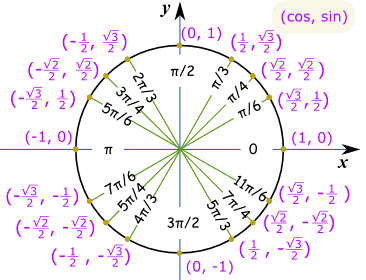
Easy Way Of Memorizing Values Of Sine Cosine And Tangent Mathematics Stack Exchange

Trigonometry Why Does Cos Pi 3 1 2 Learnmath

Trigonometry

Content Graphing The Trigonometric Functions

Find The Value Of I 2 Cos 1 1 2 Sin 1 1 2 Ii Cos 1 1 2 Sin 1 1 Iii Cos 1 Cos P 7 Cos P 17 Sin P 7 Sin P 17 Sarthaks Econnect Largest Online Education Community